Die Kleinsche Flasche, adentro, afuera, adentro...

A veces no puedo dormir pensando en cosas que se suponen resabidas. No por mí claro...jaja.

Esta vez tiene que ver con la noción del adentro y del afuera.

Todos parecen saber distinguir entre estos dos conceptos y no se les da demasiada entidad...hasta que aparecen cosas raras...

Por ejemplo, la botella de Klein ( Die Kleinsche Flasche ) o como se la llamó originalmente, la superficie de Klein (Die Kleinsche Fläche), que es la versión en cuatro dimensiones de la cinta de Möbius (superficie con 2 dimensiones, vista en nuestro universo cotidiano de 3 dimensiones).

Cinta de Möbius, superficie no orientable, donde con sólo caminar sobre la cinta,  se pasa continuamente de una cara a la otra (adentro-afuera)

La Banda de Möbius es tan interesante, porque no todos los días se está en presencia  de una superficie finita que nos muestre una sola cara y un solo borde. De modo que pasar a una dimensión superior con características similares despierta la imaginación.
Algún amigo preguntaba con cierta angustia si tenía sentido seguir probando, aún a costa de quemarse cortando y fusionando láminas, para ver si podía lograr tener, físicamente, una  botella de Klein.
Y desgraciadamente no, en cuatro dimensiones no...
Se puede tener la "proyección" en tres dimensiones, que es la tan conocida imagen

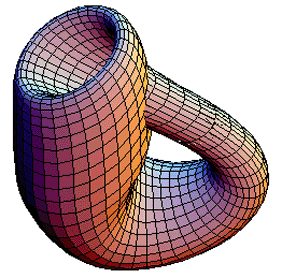Proyección tridimensional de la Botella de Klein

 Y sin embargo esta no "es" una botella de Klein, el pasaje afuera-adentro-afuera no puede darse a través de un agujero.

El pasaje de la "superficie exterior" a la "superficie interior" debe darse de modo contínuo como en la cinta de Möbius  sobre la que, caminando continuamente, en la misma dirección, uno se encuentra alternativamente "afuera", "adentro", "afuera"...

Espero que ese perseverante experimentador no esté muy quemado, o mejor aún, que haya encontrado la contraprueba.

Pero los topólogos afirman que debe ser sin agujero.
Allá ellos.






Flasche Klein Möbius superficies no orientables